Is weight, parameter and tensor interchangeable when talking about LLM model sizes?

When I first started learning about Large Language Models (LLMs), I kept seeing three words thrown around everywhere: weights, parameters, and tensors. People seemed to use them interchangeably, and I had to understand what they were exactly.
Here is the thing, I wondered, are weight, parameter, and tensor words for the same thing, especially when talking about LLM model sizes?

Parameters are brain cells
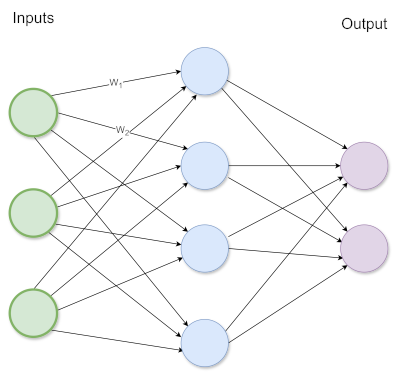
Parameters are the nodes, the little cells that make up the brain (neural network) of the AI model, basically numbers that the model learns during the training process. Very similar to how it is thought we store memories and knowledge in our own heads. When the big tech companies brag about the size of the models, with 175 billion parameter models, what they are talking about is how many points (brain cells) the model contains. Yes, they are literally bragging about how brainy their child is! 🙄 See, the more brain cells, the more potential the model has to learn!

Weight for it...
Weights are actually parameters, but with a specific role. Weights are the connections between the cells. They define how closely cells are related. In the AI world, people are using these terms interchangeably, which is OK, now that I know what they mean.

Tensors...
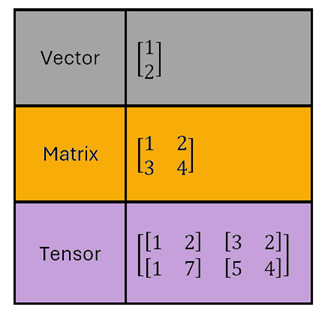
Tensors have this super great nerdy tech sound to them. Start talking about tensors at the dinner table and you have definitely reached top nerd ranking. Myself? Yes, I love the term. You may have encountered it with TensorFlow already, or if you ever sat at the dinner table with me 😄. Tensors are actually just containers (multi-dimensional arrays); they are storage boxes for our weights and parameters. They can be thought of as multi-dimensional containers that keep everything organized and easy to find.

So have we applied this knowledge to our brain cells now?

• When someone talks about model size, they usually count parameters or weights (same thing for our purposes).

• Tensors are just the way we package these numbers in the computer's memory and contain multiple weights or parameters.
  It's like counting books (parameters) vs. counting bookshelves (tensors)

Ok let me wrestle with the equation maker in Microsoft Word and show you visually a representation of the differences...

What makes things tricky fun with Tensors, is that they are defined, and used differently in different fields, computer science uses the term in a different way than in pure maths or physics.
It is also interesting to know about Tensors vs normal multidimensional arrays, are that they are designed to run on a GPU. They allow the maths on the matrices (and n-dimensional arrays) to be performed on these specialised chip sets at blazing fast speeds. They also take care of of backpropagation for you with automatic differentiation, but that is certainly getting into the heavy maths of neural networks, let us stop there!

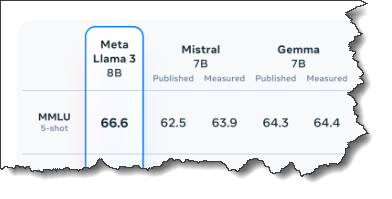
Crikey, that’s a lot of data! – Billions of parameters
So when a model is referred to as "8B" or "70B", the B means billion parameters. Depending on how the numbers in the model are stored (float32, bfloat16, or float16), the models can take up significantly different amounts of memory.
This figure does not represent the number of tensors.

So while the terms have technical differences, the AI community often uses "weights" and "parameters" interchangeably. That is OK for most discussions. Just remember that "tensors" are slightly different and are more about how we organize the data in the model!

Note
Having completed a neural networks module for my degree, I am aware the matrix maths of neural networks is much more complicated than this explanation. The average enterprise developer stepping into application of models doesn't initially need the data science backing to consume AI models. This explanation provides a working understanding for every day practical AI, sufficient for many developers and users of AI platforms.